L'emplacement de l'impact.

our déplacer les pôles il faudra, comme nous l'avons vu précédemment, que la Terre ait touchée à un endroit bien précis. L'endroit exact peut évidemment varier en fonction de l'angle avec lequel le corps céleste avait heurté la Terre. Nous ne pouvons plus vérifier avec certitude la deuxième condition. Il s'agit en fait de savoir si la Terre tournait jadis plus vite, ou plus lentement qu'aujourd'hui. A savoir, si elle tourne plus vite maintenant qu'avant, l'impact aurait dû être dans la même sens, sinon en contre-sens de la rotation.

Les possibles endroits d'impact :

Accélération de la rotation	Ralentissement de la rotation
Triangle des Bermudes	Nord-Ouest océan Pacifique
20° à 40° Nord et 60° à 100° Ouest	40° à 70° Nord et 140° à 180° Est
Le continent Australien	Au sud du Cap de Bonne espérance
20° à 40° Sud et 80° à 120° Est	40° à 70° Sud et 0° à 40° Ouest

C'est une curieuse coïncidence que la côte située devant la ville de Charleston, le triangle des Bermudes donc, démontre une structure ressemblant à un cratère ovale de sept cents sur cinq cents kilomètres. Ce qui nous laisse supposer qu'il s'agit ici d'un impact provoqué par un objet céleste d'une cinquantaine de kilomètres, heurtant la Terre en angle. En plus ce que nous pouvons voir dans les tableaux, c'est que la taille, ainsi que l'endroit correspondent à peu près à ce que nous attendons.

Un petit rappel, l'opération de déplacement de pôles est en fait le même procédé que le changement d'orientation des satellites, une petite impulsion au bon endroit suffit de lui faire changer la position. La seule différence avec les satellites est, que la Terre n'a eu aucune impulsion dans la direction opposée pour arrêter la rotation additionnelle. En fait, le résultat de l'addition de la rotation originelle et de la rotation additionnelle avait comme conséquence, que la Terre commençait à faire une rotation sur un axe différent avec une vitesse différente. Il suffirait en fait d'ajouter un composant Nord-Sud pour obtenir une rotation de la Terre sur autre un angle. Il nous reste par contre deux possibilités, une où un composant Sud-Nord aurait été ajouté en contre-sens de la rotation, puis un deuxième, où un composant Nord-Sud aurait été ajouté dans le même sens. Pourquoi Nord-Sud dans un des deux cas et Sud-Nord dans l'autre ? Il faut se rappeler, comme nous avons pu voir précédemment, qu'on avait le choix entre un ralentissement du Pôle Nord actuel, ou une accélération de l'ancien Pôle Nord, situé sur le continent du Groenland. Il y a 12 000 ans, nous avons vu, que c'était le Pôle Nord actuel qui décrivait un cercle autour d'un point qui se situe sur l'actuel Groenland. Tandis qu'aujourd'hui c'est ce point sur le continent du Groenland qui décrit un cercle autour du pôle actuel. Il fallait donc pour avoir inversé la situation, que le pôle actuel ait été ralenti, ou que l'ancien Pôle Nord de jadis, situé sur le continent du Groenland, ait été accéléré. Pour savoir la vitesse de la modification, il suffit de multiplier la vitesse de la rotation à l'équateur (463 mètres / sec.) avec le cosinus du déplacement. Mais comme on a pu le voir, ajouter cette vitesse de déplacement demande beaucoup d'énergie, qui se calcule en multipliant la masse avec la vitesse au carré.

Nous devrions nous rendre compte que les quantités d'énergie sont tellement élevées, qu'il est nécessaire de faire appel à une unité de mesure suffisamment grande. Il convient à ce stade de prendre comme référence la bombe thermonucléaire à hydrogène la plus puissante de l'histoire, la « Tsar Bomba », testée par l'Union Soviétique, qui faisait 57 mégatonnes de TNT¹.

Comme mentionné ci-dessus, nous devrions multiplier la masse par la vitesse au carré pour savoir combien d'énergie nous avons besoin pour le déplacement des pôles. La vitesse est le cosinus du déplacement multiplié par la vitesse de la rotation à l'équateur. Puis la masse est, à cause de la forme sphérique de la Terre, à peu près deux tiers de la masse terrestre. Le tableau suivant résume donc des angles différents avec les vitesses additionnelles et la quantité d'énergie nécessaire exprimée en nombre de « Tsar Bomba » de 57 mégatonnes de TNT chacune.

Tableau d'angles de déplacement avec vitesse et force nécessaire :

Angle.	Vitesse de rotation.	Nombre de bombes 'Tsar Bomba'
13°	104 m/sec.	7 435 000
14°	112 m/sec.	8 004 000
15°	120 m/sec.	8 570 000
16°	127 m/sec.	9 078 000
17°	135 m/sec.	9 650 000

Ce tableau ci-dessus ne veut pas dire qu'il suffit de faire exploser près de dix millions de bombes type « Tsar Bomba » au bon endroit pour faire un déplacement de pôles. Ça veut plutôt dire quelle quantité d'énergie serait nécessaire pour effectuer une telle opération. Ce qui était arrivé est, qu'une relative petite masse avait heurté la Terre avec une vitesse considérable. Au moment de l'impact, le résultat masse multiplié par la vitesse au carré était transformé en énergie. C'est cette énergie qui se trouvait à son tour partiellement convertie en mouvement de la Terre. Lors de cette conversion il faut probablement compter que vingt pour-cent avait été perdu sous forme de réchauffement d'eau de mer. Cette petite perte en énergie correspondait quand même à une explosion de 1 929 000 bombes de type « Tsar Bomba » .

Nous pouvons, depuis que nous connaissons la quantité d'énergie nécessaire, chercher la relation entre la taille et la vitesse de l'objet céleste. Il convient par exemple de savoir, qu'en règle générale, un impact de météorite laisse un cratère de dix fois sa taille. En d'autres mots, un objet de dix kilomètres laissera un cratère de cent kilomètres. En dressant un tableau d'objets de différentes tailles et de leurs vitesses, nous pouvons nous mettre à la recherche d'une structure ressemblant à un cratère. Puis en tenant compte, si l'objet avait heurté la Terre en angle, que le cratère en question devrait avoir une forme ovale, voire une forme elliptique.

Nous pouvons, en regardant le tableau ci-dessous, constater que les objets de cent kilomètres et plus avaient peu de probabilité d'avoir existé. En ce qui concerne les objets dont la vitesse est supérieure à quarante-deux kilomètres à la seconde, ils n'avaient guère dû exister. Ce qui nous reste, ce sont les objets dont les tailles allaient de quarante kilomètres à soixante kilomètres. Par contre, cette constatation ne devrait pas exclure les objets de plus de cent kilomètres ou de moins de trente-cinq kilomètres. Même si ces tailles sont nettement moins probables que les autres.

Correspondance entre taille et vitesse pour une déplacement de 17° : 

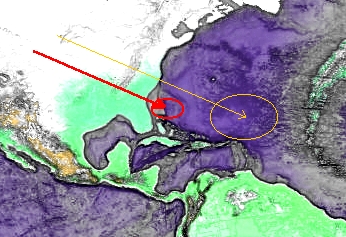En inspectant les endroits de possibles impacts d'astéroïde, nous ne pouvons trouver que quelques traces dans le triangle des Bermudes. Tout d'abord que la mer de Saragosse, au sud des îles de Bermudes, ressemble à un cratère de forme ovale d'un bon millier de kilomètres. Une deuxième formation géologique, qui ressemble fort à un cratère ovale de cinq cents kilomètres sur sept cents kilomètres, se situe juste devant le socle continental américain, dans la région de la ville de Charleston.

La zone de la ville de Charleston montre en fait d'autres curiosités géologiques. A part cette formation ressemblant à un cratère devant la côte, cette zone ne démontre pas seulement une très grande activité sismique, mais nous y trouvons également grand nombre de petits cratères. La zone avec ces petits cratères a curieusement aussi une forme d'un ovale et prolonge le trou qui se trouve devant la côte.

Nous avons en fait deux autres conditions, que nous pouvons éventuellement vérifier d'une façon indirecte. Nous avons vu que l'impact aurait pu venir, soit à contresens de la rotation de la Terre, soit dans le même sens. Il va de soi, que dans le cas d'un ralentissement, la durée d'une journée aurait dû devenir plus longue et dans le cas d'une accélération, cette durée aurait dû devenir plus courte. Nous pouvons ainsi estimer, que dans le cas d'un ralentissement, la journée aurait dû être ±23 heures à la place des vingt-quatre d'aujourd'hui. D'autre part, une accélération aurait dû avoir un effet contraire, une journée de ±25 heures à la place de vingt-quatre d'aujourd'hui. Nous devrions nous mettre à la recherche d'un calendrier mentionnent soit une année de 350 jours, soit une année de 380 jours. Un autre indice que nous pouvons éventuellement vérifier est l'horloge biologique des animaux et l'horloge biologique humaine. Il paraît que suite à une expérience menée par des scientifiques français, l'horloge biologique humaine est toujours calée sur une durée de la journée plus longue et effectivement plutôt vingt-cinq heures que vingt-quatre. L'expérience que ces scientifiques avait menée était en fait assez simple, ils ont enfermé un volontaire dans une caverne pendant plusieurs jours, sans référence avec l'extérieur. Cette personne avait ensuite un retard dans son décompte des jours. C'était comme si son horloge biologique marchait toujours avec une durée de la journée de vingt-cinq heures.

La Terre fait son tour autour du Soleil en 8 765 heures et à peu près quarante-neuf minutes. Une collision avec un objet céleste n'aurait, à cause de la différence de masse, peu d'effet sur cette durée d'orbite. Une collision aurait par contre un effet sur la durée de la journée, surtout qu'une collision est rarement au centre et va forcément modifier la rotation de la Terre. La proportion de cette modification dépend de l'endroit, de la vitesse et de l'angle de l'impact. Concernant le nombre de jours par année et la longueur de la journée, un simple calcul nous permet de constater qu'un allongement de la durée de la journée nous donne forcément moins de jours par année. Puis une durée de la journée plus courte nous donne plus de jours par année. L'importance de l'horloge biologique se trouve dans le fait que l'homme, tout comme les autres animaux se sont adaptés au fil des millénaires et milliers de générations, à une certaine durée de la journée. Et c'est justement cette durée qui se trouvait changée brutalement, sans que l'adaptation génétique ait pu avoir lieu. C'est comme cela qu'il-y encore beaucoup de gens et d'animaux, comme ce chercheur, qui vivaient, et vivent encore avec une horloge biologique de vingt-cinq heures.